BrainVoyager v23.0
Cortical Thickness Analysis
Cortical thickness and volume analysis receive increasing interest in the imaging community because it allows to relate cognitive abilities, effects of aging, and effects of diseases to (subtle) structural changes in the brain. As an example, Schneider et al. (2005) could relate cortical thickness and volume measurements in Heschl's gyrus to musical abilities.
Since BrainVoyager QX 1.7, cortical thickness can be measured in individual brains. The obtained thickness maps of multiple subjects can then be further analyzed in group studies providing both group maps as well as regions-of-interest analysis. The process begins with a segmented brain containing both the white matter / grey matter (WM-GM or simply WM) boundary as well as the grey matter / cerebro-spinal fluid (GM-CSF or simply 'pial') boundary. This file, serving as input here, can be obtained from original 3D anatomical data using either the advanced cortex segmentation tools or (preferred) the deep neural network segmentation tool.
The Cortical Thickness Analysis (CTA) tools address the following main points:
- Measurement of cortical thickness of individual segmented cortical hemispheres. This is performed first in volume space yielding cortex thickness maps (VMPs) containing the thickness measures as well as important additional information (i.e. gradient maps, see below), which are used for measuring cortical thickness on the surface in a second step. If you intend to perform laminar and columnar fMRI, only this step is necessary.
- Computation of average thickness maps across subjects and computation of statistical group difference maps. This step uses surface thickness maps (SMPs) of individual subjects as input. Averaging of thickness values across brains is based on cortex-based intersubject alignment.
- Calculation of individual and group thickness values in any region-of-interest, for example, in the frontal lobe or in the anterior bank of the central sulcus. This step also includes the statistical comparison between different regions-of-interest within a group as well as the statistical comparison of the thickness of a region-of-interest between groups. Regions-of-interest are implemented on the surface as patches-of-interest (POIs). Corresponding POIs across subjects are identified based on cortex-based alignment, which is an ideal method for the analysis of cortical thickness because it aligns very well macro-anatomical structures, such as gyri, sulci and lobes.
Measuring Cortical Thickness using the Laplace Method
How is cortical thickness measured in BrainVoyager? As Jones (2000) points out, such a measurement is not trivial since cortical thickness varies substantially across space and a simple orthogonal measurement technique - going in a fixed, orthogonal direction from one side of grey matter to the other side - may lead to erroneous thickness estimates. To avoid these problems, the cortical thickness measurements in BrainVoyager are based on the Laplace method as introduced by Jones et al. (2000).
Laplace's equation is a partial differential equation, which is used in many fields of science, notably the fields of electromagnetism, astronomy and fluid dynamics. Solutions of the equation are important in these fields because they describe the behavior of electric, gravitational, and fluid potentials. In three dimensions, the problem is to find twice-differentiable real-valued functions (phi) of real variables x, y, and z such that
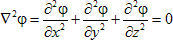
Solutions of this partial differential equation have to fulfill the constraint that the sum of the (unmixed) second partial derivatives is zero. This is fulfilled if the gradient slopes do not change along each dimension. For cortical thickness measures, we define two different "potential" (intensity) values, one at the white-grey matter (WM-GM) boundary and one at the grey-CSF (GM-CSF) boundary. A solution of the Laplace equation then results in a smooth transition of voltages (intensities) from one boundary to the other. Such a solution can be found simply by keeping the values at the boundaries fixed and by smoothing the "voltage" values in between (grey matter voxels). From the obtained smooth field, we can calculate at each voxel a gradient value. Integrating along these gradient values results in "field lines" or "streamlines". To calculate a cortical thickness value, we can start at any boundary voxel. We then check the gradient and perform a small step along the gradient direction. We then re-evaluate the gradient at the new point and perform the next step along the gradient direction. This procedure is repeated until we reach the other boundary. The sum of the performed small step sizes provides the cortical thickness value. If we go in both gradient directions ("up" and "down"), we can calculate a thickness value not only for boundary voxels but also for any voxel in between, we simply have to add up two partial streamlines.
The Laplace method is very powerful and can be used also for other interesting applications, such as the measurement of sulcal depth.
References
Schneider, P., Sluming, V., Roberts, N., Scherg, M., Goebel, R., Specht, H.J., Dosch, H.G., Bleeck, S., Stippich, C., Rupp, A. (2005). Structural and functional asymmetry of lateral Heschl's gyrus reflects pitch perception preference. Nature Neuroscience, 8, 1241-1247.
Jones, S.E., Buchbinder, B.R., Aharon, I. (2000). Three-Dimensional Mapping of Cortical Thickness Using Laplace's Equation. Human Brain Mapping, 11, 12-32.
Copyright © 2023 Rainer Goebel. All rights reserved.