Cortical Thickness and Sulcal Depth
I am happy to be able to continue my blog. I was more than two weeks very sick due to an aggressive cocktail of viruses and bacteria in my body. It started with a trip to Israel where I participated at a very nice conference. But after the 5 hour flight, a light cold became increasingly severe. From Israel, I moved to Munich to help with a BrainVoyager Training Course and it was already very painful to give my lectures. A few days later, I had to cancel a talk at a conference in Munich because I got fever. After a visit at the doctor, I had to take antibiotics for 10 days to cure a bronchitis and sinusitis. This unpleasant episode also has delayed the release of BrainVoyager QX 1.7, which should be available within a week from now.
One major new feature of BV QX 1.7 is the addition of a set of tools for the analysis of cortical thickness. This topic receives increasing interest in the imaging community because it allows to relate cognitive abilities, effects of aging and effects of diseases to subtle structural changes in the brain. The new “CTA” (Cortical Thickness Analysis) tools address the following main points:
- Measurement of cortical thickness of individual segmented cortical hemispheres.
- Computation of average thickness maps across subjects and computation of statistical group difference maps.
- Calculation of thickness values in any region-of-interest, for example, in the frontal lobe or in the anterior bank of the central sulcus. This step also includes the statistical comparison between different regions-of-interest within a group as well as the statistical comparison of the thickness of a region-of-interest between groups.
For each of these steps, a separate tab is available in the new “Cortical Thickness Analysis” dialog, called “Measurement”, “Group Maps” and “POI Analysis”. In steps 2 and 3, cortical thickness values have to be averaged across subjects, which requires a good spatial correspondence between brain regions. Since these steps work at the surface level, cortex-based alignment is used to provide a good match of macro-anatomical structures (gyri and sulci) across subjects. Step 3 requires the selection of arbitrary sub-regions of cortex, which is provided by the Patches-of-Interest (POIs) facilities in BV QX. The CTA tools, thus, built on various other features available already in the software.
How is cortical thickness measured? As Jones (2000) points out, such a measurement is not trivial since cortical thickness varies substantially across space and a simple orthogonal measurement technique - going from one side in a fixed direction to the other side - may lead to erroneous thickness estimates. To avoid these problems, the cortical thickness measurements in BV QX are based on the Laplace method as introduced by Jones et al. (2000, Human Brain Mapping, 11, 12-32).
Laplace's equation is a partial differential equation, which is used in many fields of science, notably the fields of electromagnetism, astronomy and fluid dynamics. Solutions of the equation are important in these fields because they describe the behavior of electric, gravitational, and fluid potentials. In three dimensions, the problem is to find twice-differentiable real-valued functions (phi) of real variables x, y, and z such that
![]()
Solutions of this partial differential equation have to fulfill the constraint that the sum of the (unmixed) second partial derivatives is zero. For cortical thickness measures, we define two different “potential” (intensity) values, one at the white-grey matter (WM) boundary and one at the grey-CSF (GM) boundary. A solution of Laplace’s equation then results in a smooth transition of voltages (intensities) from one boundary to the other (![]() ). Such a solution can be found simply by keeping the values at the boundaries fixed and by smoothing the voltage values in between (grey matter voxels). From the obtained smooth field, we can calculate at each voxel a gradient value (
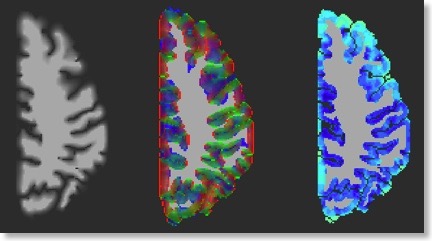
). Such a solution can be found simply by keeping the values at the boundaries fixed and by smoothing the voltage values in between (grey matter voxels). From the obtained smooth field, we can calculate at each voxel a gradient value (![]() ). Integrating along these gradient values results in “field lines” or “streamlines”. To calculate a cortical thickness value, we can start at any boundary voxel. We then check the gradient and perform a small step along the gradient direction. We then re-evaluate the gradient at the new point and perform the next step along the gradient direction. This procedure is repeated until we reach the other boundary. The sum of the performed small step sizes provides the cortical thickness value. If we go in both gradient directions (“up” and “down”), we can calculate a thickness value not only for boundary voxels but also for any voxel in between, we simply have to add up two partial streamlines. The snapshot above shows on the left side the smooth values from the WM to the GM boundary, in the middle the gradient directions (x, y, z in red, green, blue) and on the right side the obtained thickness values for all grey matter voxels.
). Integrating along these gradient values results in “field lines” or “streamlines”. To calculate a cortical thickness value, we can start at any boundary voxel. We then check the gradient and perform a small step along the gradient direction. We then re-evaluate the gradient at the new point and perform the next step along the gradient direction. This procedure is repeated until we reach the other boundary. The sum of the performed small step sizes provides the cortical thickness value. If we go in both gradient directions (“up” and “down”), we can calculate a thickness value not only for boundary voxels but also for any voxel in between, we simply have to add up two partial streamlines. The snapshot above shows on the left side the smooth values from the WM to the GM boundary, in the middle the gradient directions (x, y, z in red, green, blue) and on the right side the obtained thickness values for all grey matter voxels.
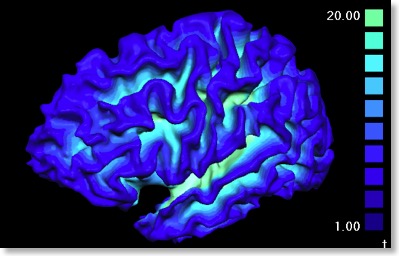
Note that the Laplace approach can not only be used to calculate the grey matter thickness but also to compute the depth of sulci. The only difference for the computation of sulcal depth is that one boundary must be the boundary of the brain and the other boundary must be the white (or grey) matter. The computed streamlines then travel from any WM point through the sulci up to the boundary of the brain and the integrated path length values result in sulcal depth measures. The snapshot on top of this blog entry shows the result of such a sulcal depth measurement as a surface map.